Modeling Instruction in Physics: Summary for Unit 3

This unit is focused on developing the model for an object moving with constant acceleration. I've always considered the model of an object moving with constant velocity to be a special case of this model. We didn't discuss that at all during this unit, and I don't know if that's because it's more desirable to think of them being 2 distinct models, or because none of us (as students) brought up the fact that a = 0 m/s/s *is* a constant acceleration. I guess that means it's more appropriate to say this unit develops the model for an object moving with constant, nonzero acceleration.

Instructional Goals we addressed:

1. Concepts of acceleration, average vs. instantaneous velocity
1. Contrast graphs of objects undergoing constant velocity and constant acceleration.
2. Define instantaneous velocity (slope of tangent to curve in x vs. t graph).
3. Distinguish between instantaneous and average velocity.
4. Define acceleration, including its vector nature.
5. Include acceleration vectors on motion maps.
2. Multiple representations (graphical, algebraic, diagrammatic)
1. Introduce stack of kinematic curves.
1. position vs. time: slope of the graph = instantaneous velocity
2. velocity vs. time: slope = acceleration, area under curve = displacement
3. acceleration vs. time: area under curve = change in velocity
2. Relate various expressions.
3. Uniformly Accelerating Particle Model
1. Domain and kinematical properties.
2. Derive the following relationships from x vs. t and v vs. t graphs.
1. definition of average acceleration
2. linear equation for v vs. t graph
3. parabolic equation for an x vs. t graph
4. displacement equation for any time interval
4. Analysis of free fall

Model Development

Again, we started the unit by making observations, this time about a cart rolling down a ramp. When we said the cart was getting faster as it went, Bryan asked us how we knew, and how we could be sure. He introduced the idea of a metronome to keep time when we suggested marking where the car was each second to see if the marks stayed the same distance apart or got further and further apart each second.

Marking the car with the metronome is a great idea, but harder than it looks (or sounds). Having 3 or 4 metronomes going at the same time on different counts can get confusing. As I was marking, I found myself anticipating the next beat, and actually marking the position early. Plus, as the car reaches the lower end of the ramp, the marks actually turn in to lines as you hurry to mark each spot. Still, it's easier to listen and mark than to try to watch a stop watch and mark. You could also take a time lapse photo, or a video, of the cart moving down the track to collect data. But that removes the physical feeling of having to move faster and faster.

In the analysis of our position vs. time data, we once again found ourselves needing to answer the question of what the coefficients of the quadratic equation meant. We used some dimensional analysis to see what the units could tell us. It's clear that the second coefficient represented a velocity - we just weren't sure what velocity it was. We spent some time considering the average velocity, the starting velocity and the ending velocity. (This also led us into some discussion of average vs. instantaneous velocity, and the introduction of "slope-ometers" (whiteboard markers) for checking the instantaneous slopes.) We discussed how we might get some velocity vs. time data from our position vs. time data. We knew we needed to find slope, and with some guidance (everything is done with subtle guidance), we came to the idea of finding the slope of two points close together, and that that slope would match the actual slope at a point in the middle. (This is a great foundation for the Mean Value Theorem for derivatives!)

Now we could develop a graph and an equation for velocity vs. time data and discuss what all of it told us. We again studied the coefficient and y-intercept and their meaning, and compared them to the values in the position vs. time equation. This is where we noticed that the intercept on the v vs. t graph and the second coefficient of the x vs. t equation were very close to being the same number. We also noticed that the first coefficient in both equations had the same units. This led us to realize that the first coefficient in the x vs. t equation was half of the first coefficient in the v vs. t equation. And thus, we could generalize both equations to see two of the standard kinematic equations.

Now that we had both x vs. t and v vs. t graphs for this new situation, we compared what we were able to read from those graphs in the last unit to what we could read from these new graphs. Everything was the same, we could just now tell that the cart was accelerating because the slope of the x vs. t graph was changing, and the v vs. t graph was no longer a horizontal line.

Because we were able to find displacement from the area under the v vs. t graph before, we did so again, writing a formula for the area. We came up with 4 different formulas, using a trapezoid, a large rectangle minus a triangle, a small rectangle plus a triangle, and three triangles. With some algebraic manipulation, we were able to show that these formulas were all equivalent to each other, and that it was related to the position equation we'd just found. It was really cool to see where all of these formulas came from. The trickiest part was to consider whether we were talking about an instantaneous time or a time interval. I'm going to have to watch myself very carefully in my class - I tend to use them interchangeably, and I can definitely see where that will confuse students.

From here, we moved to a lab extension using motion sensors. This was a great activity to get us to consider the sign of the acceleration. Usually, students think of negative acceleration as slowing down and positive acceleration as speeding up, but because sign values in physics are about direction, there's a mental shift that has to be made. So there will be confusion about why the velocity graph for slowing down in the negative direction has a positive slope (to give one example). If students aren't verbalizing that difference, it's really important to ask questions that get them to do so. I can guarantee there will be students every year who need to see that contradiction.

Model Deployment
At this point, we had our model pretty much built. Our next step was to investigate a new context for the same model: a falling object. There was some discussion ahead of time as to whether the falling stuffed pig was accelerating or not. (Why are we more afraid to step off a roof than we are a table?) There were different methods for gathering the data for this lab. My group used a motion detector, but it took some work to get a good graph. And even then, we were selective about the parts of the graph we chose to look at. (Students had better have a good reason for why they chose that section of the graph - did they compare it against what was actually happening at that time?) Other groups took slow motion videos or pictures of the object falling past a series of meter sticks. During the discussion of this lab, we all reached the conclusion that objects fall with an acceleration of 10(ish) m/s/s. (All of our acceleration values were close to 10.)

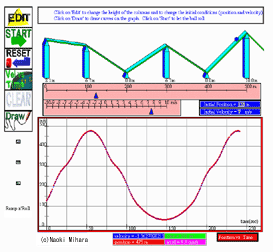
We also used several worksheets during the deployment phase. Some asked us to solve the usual numerical problems. I found myself turning to the graph more than the equations - what a difference from my normal approach! Other worksheets had us drawing position, velocity and/or acceleration graphs, given one type of graph or another. The most fun was trying to recreate a given stack of graphs using the Ramp-n-Roll applet. It was frustrating at times, but exciting when you got all 3 graphs to match. (I found it easiest to focus on the v vs. t graph, and then check the rest.)



At the end of this unit, we began to develop qualitative motion maps of an object thrown upward that returns to its starting position. It was important for us to start by just drawing the dots, and not arrows, so we could focus our first argument on how you determine the position, and where you draw the top dot. Then, once that was settled, we drew in the velocity vectors. That led to another argument about what those arrows mean, and whether there should be an arrow from the top dot to the following dot or not. Once those arguments are settled, you could start asking "what if" questions, changing the initial velocity or the time interval, to see how much the maps change. (It's a lot.) But don't do that until students are ready. Maybe wait a day.

Finally, we had our Unit 3 Practicum. We were much closer this time!